There is currently a lot of excitement around the new Essbase Hybrid Aggregation Mode. As this new feature matures, clients are starting to ask about the types of cubes that are best suited for conversion to the new calculation engine. While Hybrid Aggregation Mode is pretty amazing, a side project of mine recently reminded me of a specific class of cubes that are not yet appropriate for conversion.
First, a bit about the side project . . . I’m working on building a set of “reference” cubes that I can easily deploy in various environments to benchmark physical (and virtual) infrastructure. Imagine a set of cubes that run through a standard series of data loads, calculations and retrieves where the performance is recorded for comparison against other environments. The idea is to arrive at a “score”, so I know early in an implementation when I’m working on suboptimal hardware. For this to work, I need some really big cubes (BSO, ASO and Hybrid). And when one builds really big cubes, they are sometimes reminded of Essbase’s size limitations, because when reached . . . dimension builds fail. These limits are very nicely documented here.
The basic Essbase size limitations are pretty straight-forward:
- BSO cubes can have a maximum of roughly 1,000,000 members.
- ASO cubes can have a maximum of roughly 10,000,000 – 20,000,000 members.
Hybrid cube limitations are not specifically called out in the documentation (yet), but we can make some assumptions:
- We know that Hybrid cubes start out life as normal BSO cubes.
- We assume that BSO limits apply to Hybrid cubes. (My limited testing appears to confirm this.)
- We know that BSO cubes have lower size limitations than ASO cubes.
- Therefore, certain large ASO cubes can not be converted to Hybrid.
In addition to the basic size limitations above, there is a slightly different limit that developers are more likely to encounter:
- BSO cubes can have a maximum of 2104 stored sparse member combinations.
Here’s what makes this limit so interesting . . . the documentation (which is very, very good overall) is incorrect. BSO cubes are not limited to 2104 stored sparse member combinations. Instead, they are limited to “Two Groups of 252”stored sparse member combinations. What does that mean? How do we know the documentation is wrong? Let’s dig a little deeper.
Over 20 Nonillion Stored Sparse Member Combinations!
2104 is a very large number. It’s a smidge over 20 nonillion. Don’t know what a “nonillion” is? I didn’t either.
2104 = 20,282,409,603,651,700,000,000,000,000,000
To understand this limit, we must first understand how to calculate the number of potential stored sparse member combinations. (These are “potential” combinations until there is data at a particular intersection of members . . . then they become “actual” combinations.) To arrive at the number of potential stored sparse member combinations, simply multiply the number of stored members from each sparse dimension together.
For example:
- Sparse Dimension #1: 10 Stored Members
- Sparse Dimension #2: 30 Stored Members
- Sparse Dimension #3: 100 Stored Members
- Sparse Dimension #4: 1000 Stored Members
10 * 30 * 100 * 1000 = 30,000,000 Potential Stored Sparse Member Combinations
In other words, there are 30 million unique possible combinations of sparse members if we take one member from each of the above four dimensions.
If we were in fact limited to 2104 potential stored sparse member combinations in a BSO cube, it is unlikely that anyone would hit this limit. This is because another limit would most likely kick in first. Remember, developers can have a maximum of roughly 1,000,000 members in a BSO cube. Try arriving at 2104 potential stored sparse member combinations when you only have a million total members to work with . . . it’s possible, however it requires an unusual number of sparse dimensions.
Will the Real BSO Limit Please Stand Up?
If the 2104 limit is incorrect, what is the real limit? Luckily, Essbase returns the correct error message during a dimension build . . . it’s only the documentation that is incorrect. Here is what shows up in the Essbase application log after the dimension build fails:
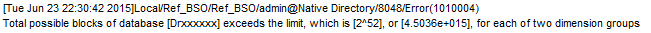
It’s easy to see how the 2104 limit was incorrectly derived. 2 * 252 = 2104, right??? Wrong.
252 = 4,503,599,627,370,500
2 * 252 = 9,007,199,254,740,990 (Note that this number is much less than 20+ nonillion or 2104.)
However, don’t be fooled into thinking that the real limit for potential stored sparse member combinations in a BSO cube is 9,007,199,254,740,990. That’s not correct either. Remember, we get two groups of 252 stored sparse member combinations. How the dimensions fall into these two groups is very important.
Show Me the Groups!
Here are the basic steps for determining whether or not you will exceed the “Two Groups of 252” limit:
- Locate the first sparse dimension (closest to the top of the outline).
- Multiply the number of stored members in this dimension with the number of stored members in the next dimension.
- Repeat until the product of stored sparse members exceeds 252 (4,503,599,627,370,500).
- Back up one dimension. The 1st sparse dimension down to this dimension makes up the first “group”. The idea is that a group’s stored member product cannot exceed 252.
- Start multiplying the stored members from each subsequent sparse dimension together. These dimensions represent the 2nd group. If the product exceeds 252 on the second group, the limit has been reached and the dimension build will fail.
Here is an example of two groups of sparse dimension members:
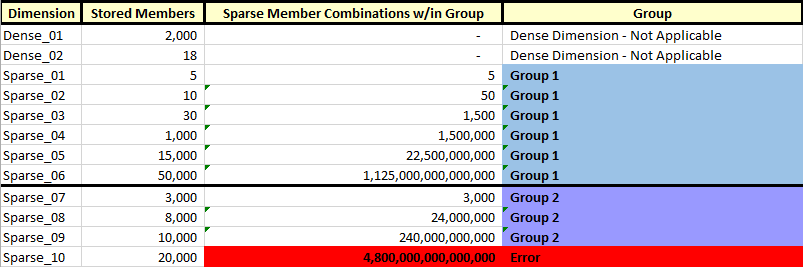
When building the dimensions in the BSO cube described above, Group 1 ends after the 6th sparse dimension (“Sparse_06”). This is because including the next dimension (“Sparse_07”) would cause the sparse member combinations in that group to exceed 252. As soon as Group 1 is as full as possible without exceeding this limit, Group 2 begins. Unfortunately, we can see that the dimension build fails at the 10th sparse dimension (“Sparse_10”), because the second group exceeds 252 and we are only allowed a maximum of two groups of 252.
Hybrid and Dynamic Sparse Members
Readers who are familiar with Essbase Hybrid Aggregation Mode may recall that one of the key design elements in a Hybrid cube involves leveraging dynamically calculated sparse parents (a general no-no in BSO, but required in Hybrid). However the “Two Groups of 252” limit is all based upon stored sparse member combinations. So could a BSO cube that failed due to this limit potentially work using Hybrid? Maybe. It all depends on how many sparse members are changed from “stored” to “dynamic” during the conversion to Hybrid Aggregation Mode.
Conclusion
If you’re thinking about taking the new Essbase Hybrid Aggregation Mode for a spin (and you should!), remember that size does matter. Some ASO cubes may not be suitable for conversion to Hybrid due to BSO size limitations. But remember that a key feature of Hybrid cubes involves setting upper-level sparse members to “Dynamic”, thus reducing the number “Stored” members in a sparse dimension. This change may create some additional “headroom” before you actually hit the “Two Groups of 252” limit with a Hybrid cube.
If you would like to hear more about this topic, please plan on attending Infratects’ Top Gun US conference on September 17-18. I’ll be presenting on Hybrid Aggregation Mode and will specifically address questions around conversions. As always, I will have a live demo.
Pop Quiz!
In the example BSO cube above, the dimension build fails at the 10th dimension. Assume the following:
- If the cube remains a BSO cube . . .
- If no members are deleted . . .
- If all dense/sparse settings remain the same . . .
- If all data storage settings remain the same . . .
What could be done to this cube to make the dimension build successful?
Tweet me the answer at @HyperionNerd.
 I have two rules for these types of presentations:
I have two rules for these types of presentations: Top Gun US 2015 has some amazing speakers and should be a great opportunity to network with Oracle product management and your EPM peers. I hope to see you there!
Top Gun US 2015 has some amazing speakers and should be a great opportunity to network with Oracle product management and your EPM peers. I hope to see you there!